Using SVM for image recognition.

Keywords: Support vector machines, image recognition.

How to separate samples if they can not be separated by a hyperplane (point in 1D, line in 2D, plane in 3D, etc.)? See MIT6_034F10_tutor05.pdf page 8 in MIT-AI2010F how to separate 2D points where class 1 more far from origin than class 2, that is any point is also a vector from origin, so their lengths (magnitudes) are separable. So instead of given vectors 2D, you should use vectors in 1D - their lengths. Decision equation in 2D is circle: \begin{align} x1^2 + x2^2 + b < 0 \mbox{ for class 1} \end{align} \begin{align} x1^2 + x2^2 + b \geq 0 \mbox{ for class 2} \end{align} But in transformed 1D the decision equation is SVM's: \(\Phi(\overrightarrow{X}) \cdot \overrightarrow{W} + b < 0 \mbox{ for class 1}\). And so does for any dimension where samples can be separated by radius, i.e. a sphere in 3D - just center samples (if origin is not in the center) and use their magnitudes (1D radiuses).

But what about images, e.g. letters? In opposite to previous example (separable by non-linear function - circle), any letter has extremely complex non-linear separating function - its contour. Is it possible to transform letter's images to get it linearly separable by only hyperplane? It seems impossible. But SVM become famous because of the best hand-written letters recognition (at that time).

It seems that LIBSVM is the best SVM library. This is C library. To compile it from source you should have GCC and Make. According to their experience we should use the best choice for many cases: radial basis function (RBF) in their interpretation: \begin{align} K(\overrightarrow{X_i}, \overrightarrow{X_j}) = e^{-\gamma\|\overrightarrow{X_i} - \overrightarrow{X_j}\|^2} \mbox{, where } \gamma > 0 \end{align} You should use their Python program (grid.py) to find the best \(\gamma\). By default it is 1/[number of features] (number of features (or attributes) is probably number of pixels for a 2D image).

Lets try LIBSVM for recognition 3 8x8 digits (see src/python/svm/dig012.py):

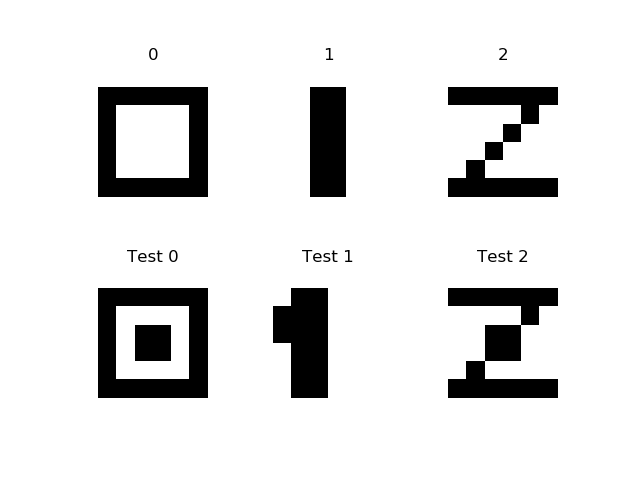
Training data (the first row of digits) in LIBSVM format is:

0 1:0 2:0 3:0 4:0 5:0 6:0 7:0 8:0 9:0 10:1 11:1 12:1 13:1 14:1 15:1 16:0 17:0 18:1 19:0 20:0 21:0 22:0 23:1 24:0 25:0 26:1 27:0 28:0 29:0 30:0 31:1 32:0 33:0 34:1 35:0 36:0 37:0 38:0 39:1 40:0 41:0 42:1 43:0 44:0 45:0 46:0 47:1 48:0 49:0 50:1 51:1 52:1 53:1 54:1 55:1 56:0 57:0 58:0 59:0 60:0 61:0 62:0 63:0 64:0
1 1:0 2:0 3:0 4:0 5:0 6:0 7:0 8:0 9:0 10:0 11:0 12:1 13:1 14:0 15:0 16:0 17:0 18:0 19:0 20:1 21:1 22:0 23:0 24:0 25:0 26:0 27:0 28:1 29:1 30:0 31:0 32:0 33:0 34:0 35:0 36:1 37:1 38:0 39:0 40:0 41:0 42:0 43:0 44:1 45:1 46:0 47:0 48:0 49:0 50:0 51:0 52:1 53:1 54:0 55:0 56:0 57:0 58:0 59:0 60:0 61:0 62:0 63:0 64:0
2 1:0 2:0 3:0 4:0 5:0 6:0 7:0 8:0 9:0 10:1 11:1 12:1 13:1 14:1 15:1 16:0 17:0 18:0 19:0 20:0 21:0 22:1 23:0 24:0 25:0 26:0 27:0 28:0 29:1 30:0 31:0 32:0 33:0 34:0 35:0 36:1 37:0 38:0 39:0 40:0 41:0 42:0 43:1 44:0 45:0 46:0 47:0 48:0 49:0 50:1 51:1 52:1 53:1 54:1 55:1 56:0 57:0 58:0 59:0 60:0 61:0 62:0 63:0 64:0

This data are already scaled, so training by default ./svm-train dig3x8x8 gives the model file:

svm_type c_svc
kernel_type rbf
gamma 0.015625
nr_class 3
total_sv 3
rho 0 0 0
label 0 1 2
nr_sv 1 1 1
SV
1 1 1:0 2:0 3:0 4:0 5:0 6:0 7:0 8:0 9:0 10:1 11:1 12:1 13:1 14:1 15:1 16:0 17:0 18:1 19:0 20:0 21:0 22:0 23:1 24:0 25:0 26:1 27:0 28:0 29:0 30:0 31:1 32:0 33:0 34:1 35:0 36:0 37:0 38:0 39:1 40:0 41:0 42:1 43:0 44:0 45:0 46:0 47:1 48:0 49:0 50:1 51:1 52:1 53:1 54:1 55:1 56:0 57:0 58:0 59:0 60:0 61:0 62:0 63:0 64:0 
-1 1 1:0 2:0 3:0 4:0 5:0 6:0 7:0 8:0 9:0 10:0 11:0 12:1 13:1 14:0 15:0 16:0 17:0 18:0 19:0 20:1 21:1 22:0 23:0 24:0 25:0 26:0 27:0 28:1 29:1 30:0 31:0 32:0 33:0 34:0 35:0 36:1 37:1 38:0 39:0 40:0 41:0 42:0 43:0 44:1 45:1 46:0 47:0 48:0 49:0 50:0 51:0 52:1 53:1 54:0 55:0 56:0 57:0 58:0 59:0 60:0 61:0 62:0 63:0 64:0 
-1 -1 1:0 2:0 3:0 4:0 5:0 6:0 7:0 8:0 9:0 10:1 11:1 12:1 13:1 14:1 15:1 16:0 17:0 18:0 19:0 20:0 21:0 22:1 23:0 24:0 25:0 26:0 27:0 28:0 29:1 30:0 31:0 32:0 33:0 34:0 35:0 36:1 37:0 38:0 39:0 40:0 41:0 42:0 43:1 44:0 45:0 46:0 47:0 48:0 49:0 50:1 51:1 52:1 53:1 54:1 55:1 56:0 57:0 58:0 59:0 60:0 61:0 62:0 63:0 64:0

It says that there are 3 classes and 3 support vectors for each class. The gamma is exactly 1/64.

Prediction for all test samples gives 100% accuracy prediction, even for shifted on 1 pixel left 1:

./svm-predict dig3x8x8-1.t dig3x8x8.model  dig3x8x8-1.t.predict
Accuracy = 100% (1/1) (classification)

The results really impress, despite of the digits are not hand-written. What is the trick? Maybe because of the dimension size is 64 plus transforming with RBF? And we get linearly separable by only hyperplane data.

But how to found RBF for sample from RBF for kernel? Example MIT6_034F10_tutor05.pdf page 8 in MIT-AI2010F says: \begin{align} K(\overrightarrow{U}, \overrightarrow{V}) = 2 \|\overrightarrow{U}\| \|\overrightarrow{V}\| \Rightarrow K(\overrightarrow{U}, \overrightarrow{V})=\Phi(\overrightarrow{U})\Phi(\overrightarrow{V}) \Rightarrow \Phi(\overrightarrow{X}) = \sqrt{2} \|\overrightarrow{X}\| \end{align} i.e. how to decompose the RBF kernel into a dot product of samples RBF?

But kernel is actually dot-product of two vectors, i.e. maybe decision equation is: \begin{align} K(\overrightarrow{X}, \overrightarrow{W}) + b < 0 \mbox{ for class 1} \end{align}

But how to find b by rotating coefficient vector W, i.e. in the same way as in the first article? That is heck if: \begin{align} b = -K(\overrightarrow{X}, \overrightarrow{W}) \end{align} For decision points in the example X4cl1(2,2) and X5cl2(-3,-3): bH4=-2*sqrt(8)*1=-5.656854249, bH5=-2*sqrt(18)=-8.485281374. That is (b = bH2 - (bH2-bH1)/2) -> b=-8.485281374 - (-8.485281374+5.656854249)/2= -8.485281374 + 2.828427125/2 = -7.071067811. That is, it's different from -5 in the example.

Lets try classification for this MIT example with b=-7.071067811 and W={0, 1}, so for X(-2,-2) -> 2*sqrt(8)*1 - 7.071067811 = -1.414213562, i.e. class 1, and for X(-2,-3) -> 2*sqrt(13)*1 - 7.071067811 = 0.14003474, i.e. class 2. That is it works.

See svm/test_2dmit.py that tests that.

That means that we can find separating hyperplane (W and b) by rotating W with using any kernel without knowing "what is transformed data? And what is dimension size of transformed space?". Here rotating W in 64D in growing margin direction seems to be feasible.

If you look inside LIBSVM's svm.cpp, then you will see that sample rows data are treated as vectors, so here is 64D vector. If we treat 64 points in 2D of a digit as one point in 64D, then we have 3 64D samples (training data), and 3 64D samples of testing samples. Any two different points of any dimension are definitely linearly separable.

So, we have 3 training samples, i.e. 3 classes. How to classify a test sample in case of number of classes is greater than two? Definitely by finding margins between a test sample and training samples, and the minimum margin is decision, i.e. points of the same class must be close to each other.

Test svm/test_dig012.py do this. Unfortunately, in case of using linear kernel (without transformation), the test sample 2 is close to the training sample 0! But RBF with gamma=1/64 works fine.

Conclusion

LIBSVM with linear kernel works fine for this 3 digits example.

Method MIT-AI2010F, MIT6_034F10_tutor05.pdf, page 6 - solving linear system equations with linear kernel also work fine, see python/svm/test_dig012a.py

Method - "rotating coefficient vector for finding margin" can't find global maximum for many-dimensional samples (64D here) at this time. For example, the margin between the training 0 and 1 by "vector rotating" is 0.73029674, but by "solving system equations" it is 1.6329931618554523.

References: